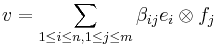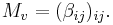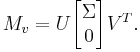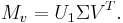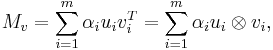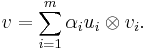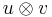Schmidt decomposition
In linear algebra, the Schmidt decomposition (named after its originator Erhard Schmidt) refers to a particular way of expressing a vector in the tensor product of two inner product spaces. It has applications in quantum information theory and plasticity.
Contents |
Theorem
Let 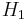 and
and 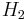 be Hilbert spaces of dimensions n and m respectively. Assume
be Hilbert spaces of dimensions n and m respectively. Assume 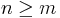 . For any vector
. For any vector  in the tensor product
in the tensor product  , there exist orthonormal sets
, there exist orthonormal sets 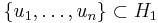 and
and 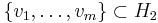 such that
such that 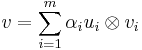 , where the scalars
, where the scalars 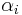 are non-negative and, as a set, uniquely determined by
are non-negative and, as a set, uniquely determined by  .
.
Proof
The Schmidt decomposition is essentially a restatement of the singular value decomposition in a different context. Fix orthonormal bases 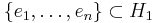 and
and 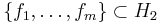 . We can identify an elementary tensor
. We can identify an elementary tensor 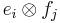 with the matrix
with the matrix 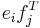 , where
, where 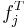 is the transpose of
is the transpose of 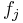 . A general element of the tensor product
. A general element of the tensor product
can then be viewed as the n × m matrix
By the singular value decomposition, there exist an n × n unitary U, m × m unitary V, and a positive semidefinite diagonal m × m matrix Σ such that
Write 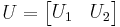 where
where 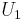 is n × m and we have
is n × m and we have
Let 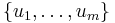 be the first m column vectors of
be the first m column vectors of 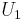 ,
,  the column vectors of V, and
the column vectors of V, and  the diagonal elements of Σ. The previous expression is then
the diagonal elements of Σ. The previous expression is then
which proves the claim.
Some observations
Some properties of the Schmidt decomposition are of physical interest.
Spectrum of reduced states
Consider a vector in the form of Schmidt decomposition
Form the rank 1 matrix ρ = v v*. Then the partial trace of ρ, with respect to either system A or B, is a diagonal matrix whose non-zero diagonal elements are |αi |2. In other words, the Schmidt decomposition shows that the reduced state of ρ on either subsystem have the same spectrum.
In the language of quantum mechanics, a rank 1 projection ρ is called a pure state. A consequence of the above comments is that, for bipartite pure states, the von Neumann entropy of either reduced state is a well defined measure of entanglement.
Schmidt rank and entanglement
For an element w of the tensor product
the strictly positive values 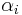 in its Schmidt decomposition are its Schmidt coefficients. The number of Schmidt coefficients of
in its Schmidt decomposition are its Schmidt coefficients. The number of Schmidt coefficients of  is called its Schmidt rank.
is called its Schmidt rank.
If w can not be expressed as
then w is said to be an entangled state. From the Schmidt decomposition, we can see that w is entangled if and only if w has Schmidt rank strictly greater than 1. Therefore, a bipartite pure state is entangled if and only if its reduced states are mixed states.
Crystal plasticity
In the field of plasticity, crystalline solids such as metals deform plastically primarily along crystal planes. Each plane, defined by its normal vector ν can "slip" in one of several directions, defined by a vector μ. Together a slip plane and direction form a slip system which is described by the Schmidt tensor 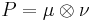 . The velocity gradient is a linear combination of these across all slip systems where the scaling factor is the rate of slip along the system.
. The velocity gradient is a linear combination of these across all slip systems where the scaling factor is the rate of slip along the system.